図1
model of , model forとその教材例
森本 貴彦
(典拠:森本貴彦・礒田正美(2003).真実的数学教育論に見るモデル論;生徒が意味理解を深めるための媒介表現,教育科学数学教育1月号,104-107)
model ofとmodel for
現実的数学教育(RME)(以下、RMEと書く)は、「人間の活動としての数学」という考え方を基本としている。つまり、児童・生徒は活動を通して算数・数学を経験する必要があるということである。また、RMEでは、その活動は、現実的な状況における児童・生徒の実経験から出発すべきとしている。つまり、フォ−マルな数学的知識は、現実的な状況でのインフォ−マルで具体的な経験から出発し,構成されるのでなければならないとしている。この状況には、日常的な現実性をもつものやフォ−マルな数学それ自身も含まれる。(高橋、2001)
また、RMEは、「導かれた再発明」と「漸進的な数学化」、「教材が本来備える数学現象を、応用と生徒にとっての真実性(現実感)という視野から教材研究すること」、「インフォ−マルな知識とフォ−マルな知識との間にある隔たりを、自己発達的modelで橋渡しするもの」という3つの原理によって説明される。ただし、ここでのmodelとは、子どもが持っている知識とフォ−マルな数学的知識の間にあるギャップを埋めるための道具である。(森本・礒田、2002)
これらの特色や原理から、RME理論では、ボトムアップの考え方が追求される。ボトムアップの考え方とは、子ども達が、自分でmodelを作って、そのmodelをフォ−マルな数学的知識を獲得していく土台として使うという考え方である。そのボトムアップの考え方は、次のような流れで表すことができる。
最初に文章題としての問題状況が子どもに与えられ、子どもは、その状況を表すmodelを作る。その後、子どもは、modelを用いてその問題状況を解決しようとする。ここでのmodelは、状況に依存したものである。子どもが問題状況を解決しようして、いろいろな方略や知識を持ち込むことを通して、このmodelが一般化され、状況には依存しない独立したものになっていく。その結果、そのmodelは、新たな状況を数学的に理由付けをするためのmodelとしてはたらくことができるようになる。
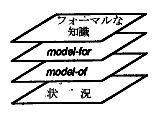
このボトムアップの考え方の特徴は、4つのlevel(図1を参照)にわけることができるmodelの質によって明らかとなる。ここで、RMEの中で、modelは、最初はフォ−マルではない表現や考え方の中から生じていることを注意しておく。
最初のlevel(状況)では、子どもが考えていることは、現実生活と関係がある。この中で、子どもは、状況にあった知識や方略を持ち込み、この状況下で応用してみる。
 図1 |
第2のlevel(model-of)では、与えられた状況での問題を解くために、子どもは、状況を表すmodelを作る。その中で、第1のlevelで考えていた知識や方略を書いたものとしてmodelに表せるようになる。しかしながら、このlevelでのmodelは、状況に依存している。
第3のlevel(model-for)では、子どもは、数学的視点から方略の方へ焦点を当てる。方略の方へ焦点を当てることで、modelはある数学的知識のためのmodelとなる。また、このlevelで、子どもはmodelを状況に依存せずに考えることができるようになる。
第4のlevel(フォ−マルな知識)では、子どもはフォ−マルな数学的知識を獲得しているのである。
ただし、ここで示したlevelは、局所的なlevelであることを注意しておく。つまり、ここに示しているlevelは、特別な話題、基本的な事実、2数の加法や減法、書かれている演算方法、分数などの子どもの理解に依存している。
また、このlevelは、ある意味、絶対的なものではない。それは、異なるlevelが、分離されているというものではないからである。この考え方は、子どもは、より低いlevelに戻ることができるというものであり、この考え方では、低いlevelは、高いlevelに組み込まれなければならない。
教材例
MIC(Mathematics in contextの略。以下MICとする)プロジェクト(1996a,1996b)は、図2のような状況を設定し、次の4つの質問をすることで、子どもが代入法や加減法についての数学的知識を得ていくことを示している。
 図2 |
(1)帽子と傘の1つの値段を計算せずに、どちらの値段が高いか考えてください。
(2)帽子と傘の関係を表す図を描いて、そのときの合計金額を書いてください。
(3)帽子だけ、もしくは傘だけの値段の関係を考えて、その値段を書いてください。
(4)帽子と傘の1つの値段は、いくらか書いて下さい。
MICプロジェクト(1994)は、(2)の問いに対し、図3に示すような関係を表す図が示され、このときの考え方をもとに、(3)をCやUといった文字を使いながら解くことを示している。その結果、(4)のような問いに対し、解答ができることを示している。
 図3 |
また、この解法をするときに、図5のような図を用いて考えることもあるだろうとしている。
 図4 |
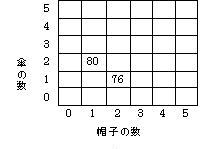 図5 |
このとき、図6で示したような操作によって、この問いに答えていくことを示している。
図6 図7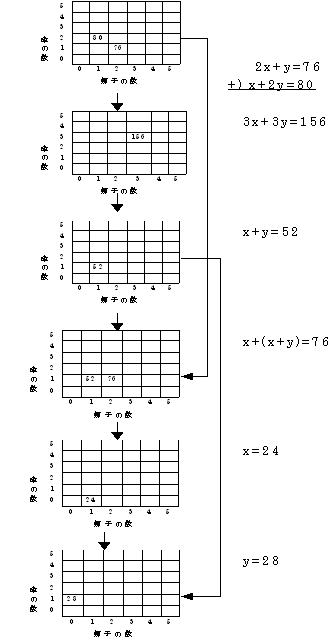 図6 図7 |
以上を、model-of ,
model-forで分析する。
まず、図3や図5は、図2の状況のmodelとなる。図2の状況で考えていた知識や方略を書いたものとしてmodelの中に表している。ただし、これはmodelの一例であり、他にもmodelは考えられることを注意しておく。
さらに、図3は、帽子だけや傘だけの場合の値段を考えるためのmodelとなる。つまり、子どもは、数学的視点から帽子だけや傘だけにするための方略の方へ焦点を当てることとなる。このように帽子だけや傘だけにするための方略の方へ焦点を当てることで、図3は、図4の式を用いた解法のためのmodelとなる。同様に、図6は、帽子1つ、傘1本の値段を求めるためのmodelとなる。つまり、子どもは、数学的視点から帽子1つや傘1本にするための方略の方へ焦点を当てることとなる。このように帽子1つや傘1本にするための方略の方へ焦点を当てることで、図6は、図7の式を用いた解法のためのmodelと考えられる。
その結果として、子どもは、代入法や加減法といった数学的知識を獲得している。
主要参考文献:
礒田正美(1996).テクノロジーの進化と米国の教育改革からみた日本の課題(2)―米国が新世紀へ向けて取り組むもの―,教育科学算数教育,5月号 75-79.
高橋等(2001).和蘭フロイデンタ−ル研究所における数学教育の理論と素材,平成13年度研究と実践
森本貴彦・礒田正美(2003).真実的数学教育論に見るモデル論;生徒が意味理解を深めるための媒介表現,教育科学数学教育1月号 No.542,104-107
文部科学省(2002). 方程式変形の意味, 個に応じた指導に関する指導資料,教育出版所収, 58-60
Gravemeijer, K.P.E.(1994). Developing Realistic Mathematics Education,
Freudenthal Institute, Utrecht University, Utrechit.
Mathematics
in Context (1996a).Mathematics in
Context Sampler,Britannica(P31),Encyclopedia
Britannica Educational Corporation
Mathematics in
Context(1996b).Britannica
Mathematics System;Mathematics in
Context Comparing Quantities,Britannica(P18),Encyclopedia Britannica Educational Corporation
Mathematics in
Context(1994).Comparing
Quantities,Britannica(PT10,PT18),Encyclopedia Britannica
Educational Corporation